关系代数
计算机科学家 Codd 对关系代数的形成作出了很大的贡献,他的代数的六个原始运算是「选择」、「投影」、「笛卡尔积」、「并集」、「差集」、「重命名」。
Select
相当于 sql 中 where 的功能。
一般形式:
$$ \sigma_{verb}(relationship) $$
选择谓词一般是逻辑表达式,可以是连词连接(也可以没有连词)的多个比较语句。
Projection
相当于 sql 中 select 的功能。
一般形式:
$$ \Pi_{fields}(relationship) $$
从关系中选出若干属性列组成新的关系,在这种选择过程中可能会减少一些列(没有被选中或者出现了重复)。
Join
连接可以分为自然连接、等值连接、外连接等。
等值连接,从关系 R 和 S 的广义笛卡尔积中选取 A 、B 属性值相等的那些元组,一般形式:
$$ R\bowtie_{A=B}S $$
自然连接, 连接时两个关系中比较的分量必须是同名的属性组,并在结果中把重复的属性列去掉。一般形式:
$$ R\bowtie{S} $$
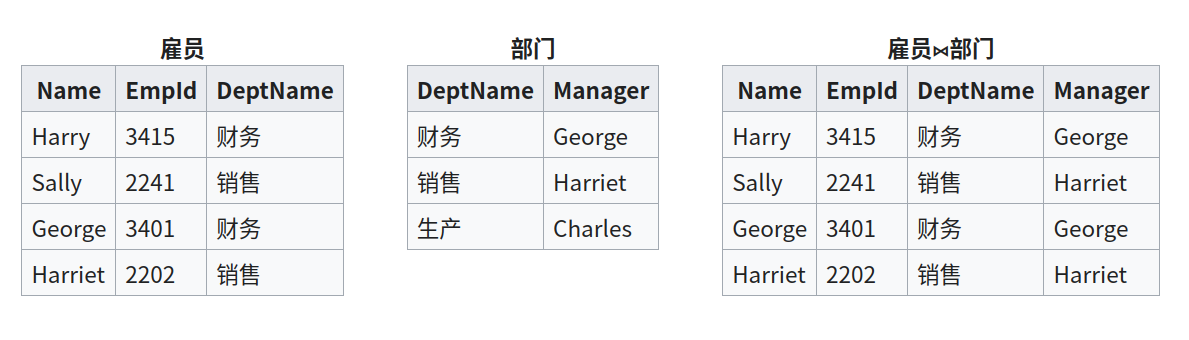
自然连接时会出现 R 中的某些元组在 S 中不存在公共属性上值相等的元组,所以出现了「悬浮元组」,如果保留它们,未知的属性填上 NULL ,这就是「外连接」。如果只保留左边关系中的悬浮元组就是「左外连接」,反之就是「右外连接」。
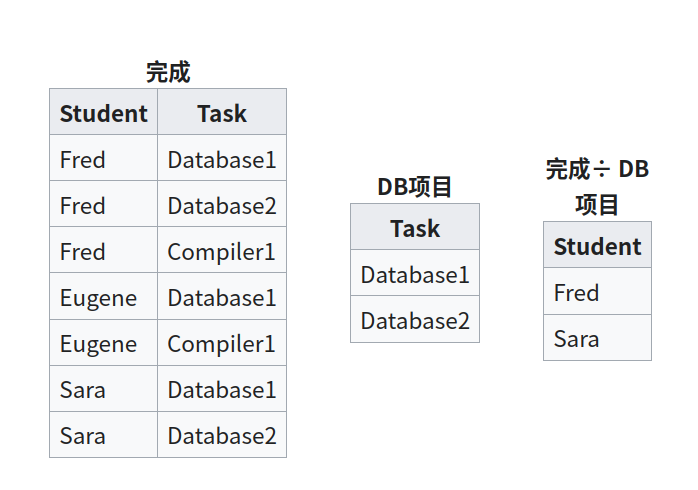
Divsion
其结果由 R 中元组到唯一于 R 的属性名字(就是说只在 R 表头中而不在 S 表头中的属性)的限制构成,并且它们与 S 中的元组的所有组合都存在于 R 中。一般形式:
$$ R\div{S} $$
Rename
一般形式:
$$ \rho_{a/b}(R) $$
把所有元组中的 b 字段改成 a 字段。相当于 sql 中的 as 。
PS:
关系的完整性:
- 实体完整性(主码不能为空)
- 参照完整性(外码要么为空要么存在于参照关系中)
- 用户定义完整性(要遵照用户的定义,例如人数不能为小数等)