最近在上大数据分析的课程,老师使用的是斯坦福大学的教材和 PPT ,感觉挺有趣的,记录一下其中的一些算法。
背景
很多问题可以被归化为寻找相似集合的问题:
- 论文差重
- 寻找购买相似商品的人群
- 寻找有相似特征的图片
不妨将这次的目的设置为:给定大量的文档,发现其中有抄袭嫌疑的
但问题是,一个集合中的元素非常多,如果要直接比对,其复杂度可以达到 $O(N^2)$ ,这在大数据尺度明显是不能接受的。
前置知识
数据之间的距离:
也可以说是用数据之间的相似度,一般距离越远,相似度越低
- 向量的思想:使用角度度量
- 集合的思想:使用雅卡尔距离度量
- 点的思想:使用欧氏距离度量
雅卡尔指数可以度量有限样本集合的相似度,定义为两个集合交集大小和并集大小之比:
$$ J(A, B) = \frac{\lvert A \cap B\rvert}{\lvert B \cup A\rvert} = \frac{\lvert A \cap B\rvert}{\lvert A \rvert + \lvert B \rvert - \lvert A \cap B \rvert} $$
雅卡尔距离用于度量样本集之间的不相似度,定义为 1 减去雅卡尔系数:
$$ d_J(A, B) = 1 - J(A, B) = \frac{\lvert A \cup B \rvert - \lvert A \cap B \rvert}{\lvert A \cup B \rvert} $$
也可以叫雅卡尔距离为两集合的对称差。
哈希函数是一种从任何数据中创建小的数字「指纹」的方法。
我们如果能够找到一种哈希函数,可以在压缩集合成为「指纹」的同时保留其特征,能够用于比较集合之间的相似度,就可以减小计算量了。这也就引出了 Min-Hash 这个算法。
Shingling
何为 Shingling
将文档转化为单词的集合。
如何转化是个问题,可以有以下的方法:
- 直接将文档拆分成很多个单个单词的集合
- 从文章中提取出关键单词
但以上两种方法都会损失掉单词的顺序信息。而这里要介绍的方法 Shingling 就可以避免。
这里使用的单词 Shingling 意思为「叠瓦」,非常有意思。说起「叠瓦」,可能会让人想到「叠瓦盘」。
SMR 叠瓦式磁盘是一种采用新型磁存储技术的高容量磁盘。SMR 盘将盘片上的数据磁道部分重叠,就像屋顶上的瓦片一样,这种技术被称为叠瓦式磁记录技术。该技术在制造工艺方面的变动非常微小,但却可以大幅提高磁盘存储密度。

在这里的 Shingling 也是类似的,举个例子:
文档 $D_1 = abcab$ ,使用 2-shingles 就可以获得 $S(D_1) = {ab, bc, ca}$
如此一来就可以保留原来文档中单词的顺序信息。
对 Shingle 压缩
由于两篇文档大部分的 Shingle 都会是不同的,因此可以使用 Hash 压缩 Shingle 到相同的宽度的数字类型。
之后当我们需要比较两个 Shingle 集合的相似程度时,就可以使用之前的雅卡尔距离来估算。
不过这样还是有很大的计算量,我们需要下文说的 Min-Hash 算法
- 对于短篇,k 可以取 5
- 对于长篇,k 可以取 10
仅作参考,要依据具体情况取舍
Min-Hash 算法
需求
使用雅卡尔算法比较 Shingle 的哈希依然是缓慢的。假设有 N 篇文档,则需要比较 $N(N-1)/2$ 次,当 $N = 1 million$ 时,需要比较 $5 * 10 ^11$ 次,以一天有 $10^5$ 秒,每秒可以比较 $10^6$ 估算,这将花费五天。如果 N 再大一个数量级,将会花费超过一年的时间。
Min-Hash 的思想,将大的集合转换成小的「签名」,每个签名中都包含了可以计算相似程度的信息。
首先需要将集合转换为位数组(0 和 1 组成),0 代表集合中没有这个元素,1 代表集合中有这个元素。
如此一来,交集就是「按位与运算」,并集就是「按位或运算」。
再将集合转换为矩阵,每一行表示某一元素(shingles)在不同集合(documents)中是否存在。换言之,每一列表示某一集合包含了哪些元素。
| D1 | D2 | … | Dn | |
|---|---|---|---|---|
| E1 | 0 | 0 | … | 1 |
| E2 | 1 | 1 | … | 0 |
| … | … | … | … | … |
| En | 0 | 1 | … | 0 |
假设有一个哈希函数 h ,可以满足:
- $h(C)$ 足够小,可以将大量的 shingles 放入内存中
- 签名 $h(C_1)$ 与 $h(C_2)$ 的相似程度等同于 $sim(C_1, C_2)$
$sim(C_1, C_2)$ 表示 $C_1$ 和 $C_2$ 的雅卡尔系数 $\frac{\lvert A \cap B\rvert}{\lvert B \cup A\rvert}$
理想状态下,我们找到的函数 $h(\cdot)$ 满足:
- 当 $sim(C_1, C_2)$ 很高时,有很大概率 $h(C_1) = h(C_2)$
- 当 $sim(C_1, C_2)$ 很低时,有很大概率 $h(C_1) \neq h(C_2)$
基本思路
选择一个可以将集合打乱的随机函数 $\pi$ ,它做到 $Pr(h_{\pi}(C_1) = h_{\pi}(C_2)) = sim(C_1, C_2)$ ,满足了我们的需求。
证明
证明一:
集合 $X$ 是一个文档,$y \in X$
$Pr[\pi(y) = min(\pi(X))] = 1/\lvert X \rvert$
这里的 $\pi(y) = min(\pi(X))$ 表示在使用 $\pi$ 打乱 X 后,X 中的元素 y 排在第一位。由于每个元素在随机打乱后排在第一位的概率都是均等的,因此等式右边是 $1/\lvert X \rvert$ 。
容易得到 $Pr(min({\pi}(C_1)) = min({\pi}(C_2))) = \frac{\lvert A \cap B\rvert}{\lvert B \cup A\rvert} = sim(C_1, C_2)$
证明二:
可以将两个集合中是否有某种公共元素的情况分为四类
| D1 | D2 | |
|---|---|---|
| A | 1 | 1 |
| B | 1 | 0 |
| C | 0 | 1 |
| D | 0 | 0 |
假设 [a-d] 表示这四类情况的个数
可以发现 $sim(C_1, C_2) = a/(a +b +c)$
如果将两个集合以相同的方式打乱,再从上向下扫描,第一个碰到的含有 1 的行是 A 类,则说明 $h(D_1) = h(D_2)$ 。
示例
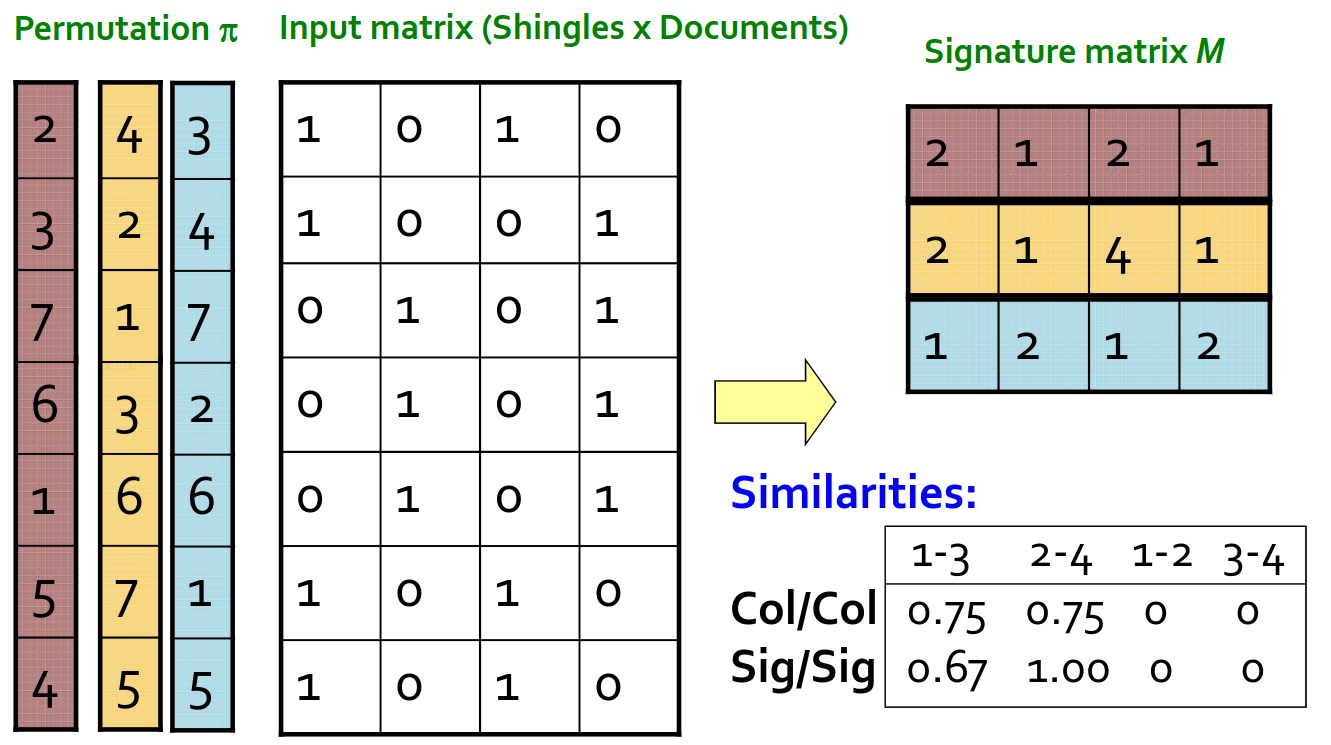
如果我们取 100 个 $\pi$ 函数用来打乱,可以为每个文档生成 100 个签名,那就可以把大量的数据压缩到可以接受的程度了。
在书中有关于 Min-Hash 实现时需要注意的问题,可以以后再水一篇博客
Locality Sensitive Hashing
基本思路
找到相似度至少为 $s$ 的文档。
即使我们已经将所有的文档转换成了很小的签名,然而文档一一配对比较的数量还是太多了,我们依然需要「哈希」和「桶」这两位老朋友。
可以使用一个函数 $f(\cdot)$ ,$f(x, y)$ 可以分辨 x 和 y 是不是相似文档的候选者。
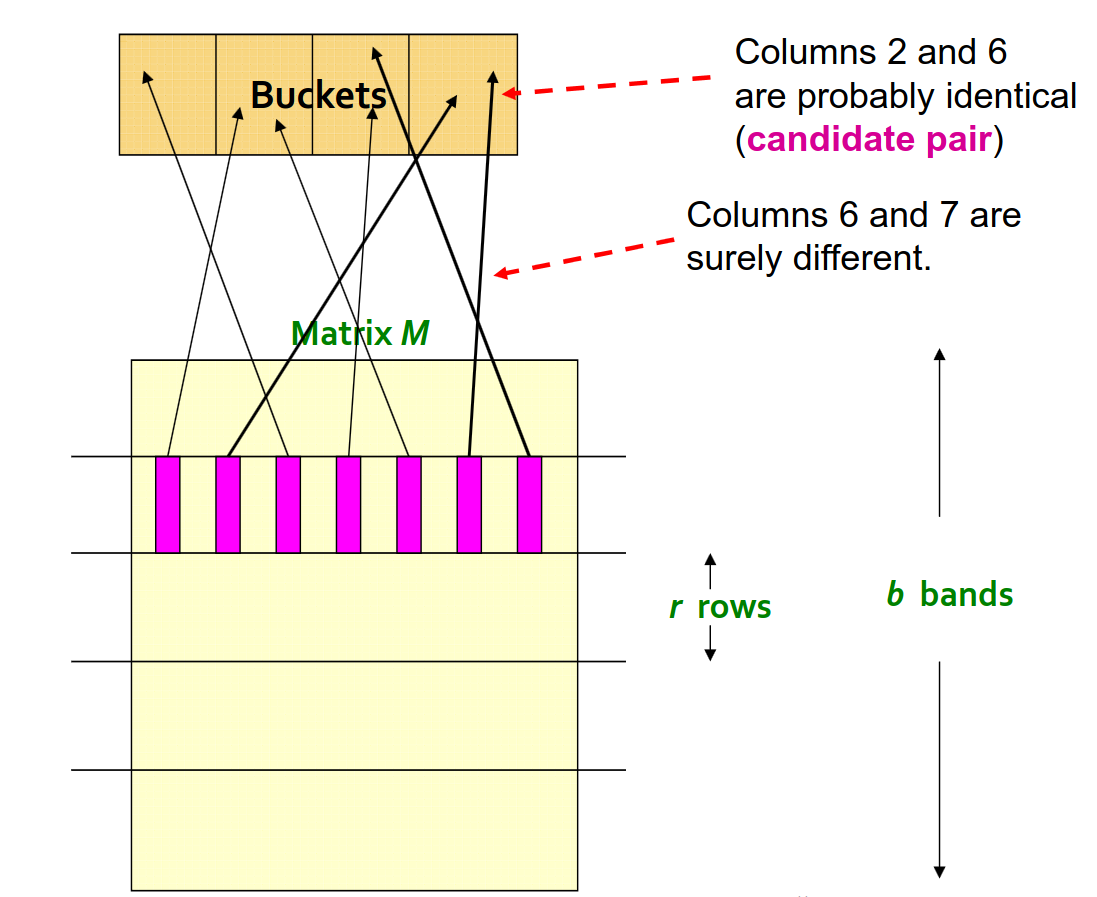
- 使用哈希函数将矩阵的列分装到不同的「桶」中
- 所有装在相同的「桶」中的文档是候选者
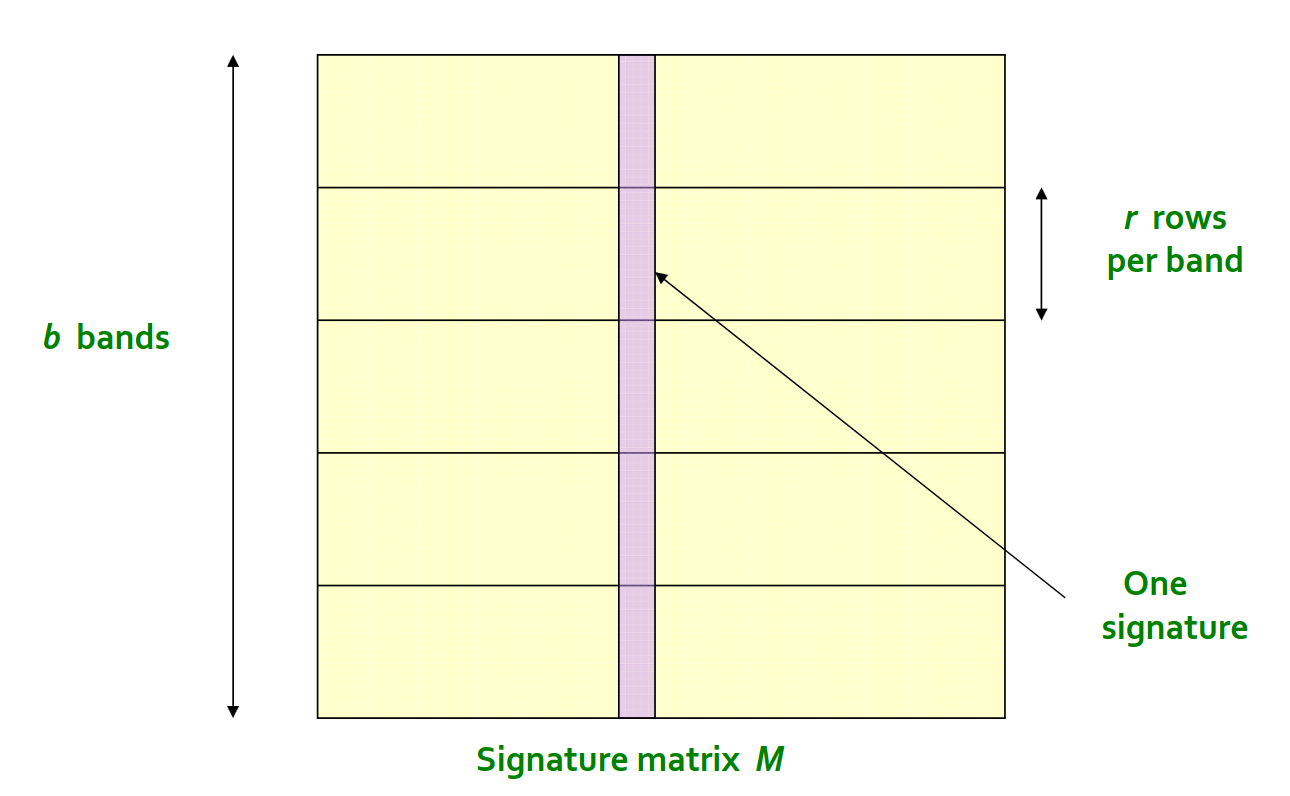
我们可以把一列分成不同的条带(band),然后进行多次哈希操作。
分成更小的条带作用是提高效率
只要有一次被分配到相同的「桶」,就可以成为候选者
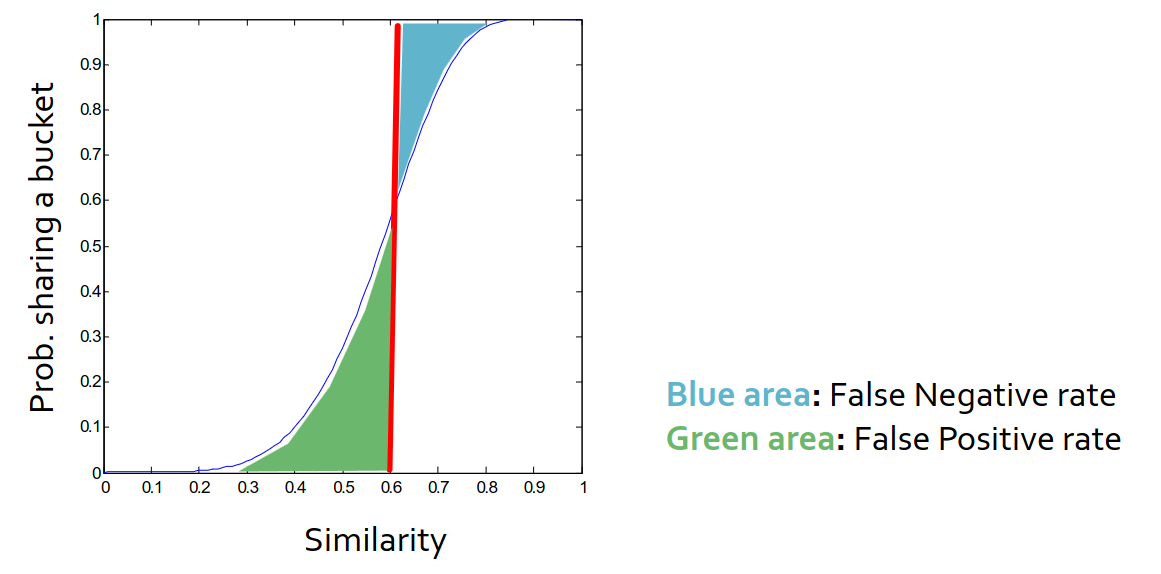
「假阴性」和「假阳性」
「假阴性」:本应被选入而没有被选入
「假阳性」:本不应被选入而被选入
- 在一个条带中的 r 行都匹配的概率为 $s^r$
- 在一个条带中至少有一行不匹配的概率为 $1 - s^r$
- 在所有条带中都有至少一行不匹配的概率为 $(1 - s^r)^b$
- 至少有一个条带的 r 行都匹配(成为候选者)的概率为 $1 - (1 - s^r)^b$
以 s 为横坐标,成为候选者的概率为纵座标,b 和 r 为常量,可以获得一条 S 型曲线。
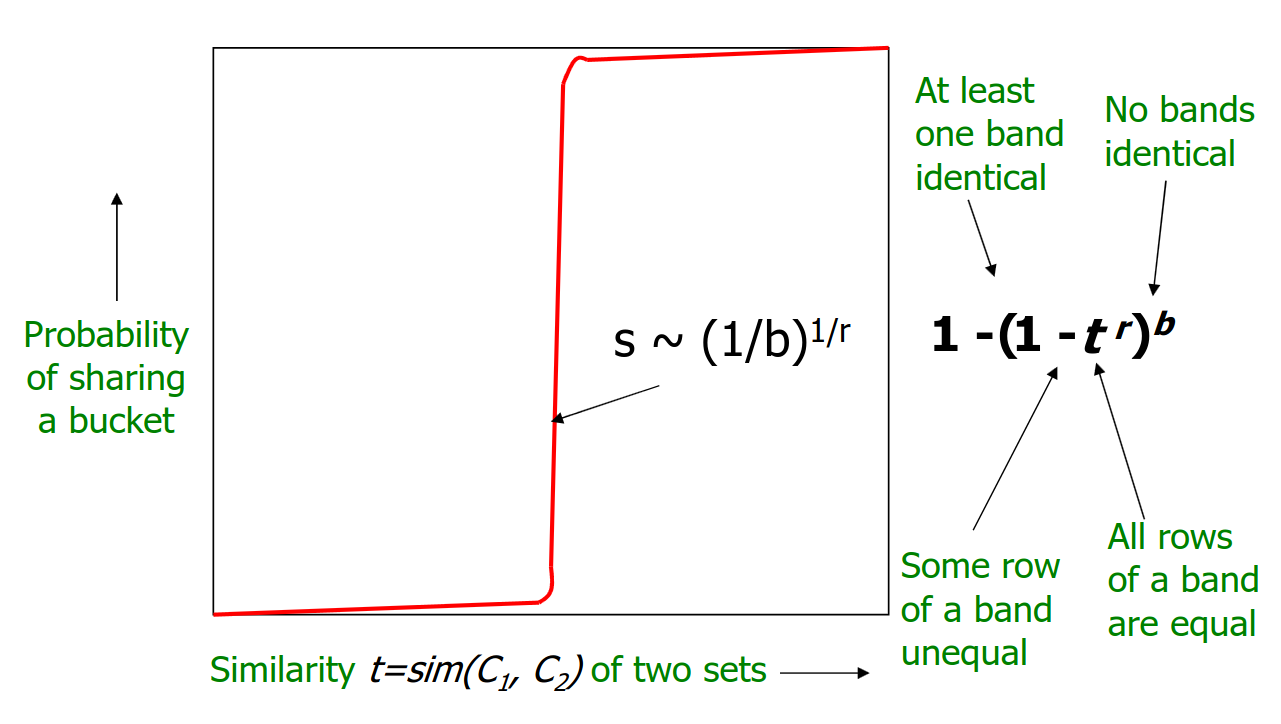
当 b 取值为 1 时,S 型曲线将会退化成为过原点的直线
取候选者概率为 0.5 ,即 $1 - (1 - s^r)^b = 1/2$
计算得到 $s = (1 - (\frac{1}{2})^{\frac{1}{b}})^{\frac{1}{r}}$
由于 $(\frac{1}{2})^{\frac{1}{b}}$ 比较接近 0 ,可以利用等价无穷小来估算 $s \sim (\frac{1}{b})^{\frac{1}{r}}$
在我们的场景下(不可放过抄袭),好的条带划分应该减少假阴性并平衡假阳性的数量。
假设划分成为 b 个条带,每个条带有 r 行,假设需要比较的两列相似度为 s 。