C++

面试时遇到的一道题：给出给出 n 个数，求出前 k 小的数字。 输入是 n + 1 行： 第一行是 n 和 k 之后 n 行是这个数列 输出是 k 个数。 当时没想出来怎么做，直接嗯排序，然后输出，OJ 的时限比较宽容，竟然过了😄。 ...

自己的 Wi-Fi6 漏油器用着还行，校园网带宽可以跑满，但是我的这个型号并不能刷 openwrt ，所以不能 ssh 连接，更不能在上面跑同学们写的那些自动认证脚本。 去年折腾 Arduino 和 nodemcu 时想到可以利用 esp8266 的联网功能让它来代替进行认证工作。 ...

最近看到了一些关于侵入式和非侵入式链表的讨论，决定研究一下它们两个。 侵入式和非侵入式链表的区别 这里的侵入是相对于链表的指针域来说，所以最主要的区别就是非侵入式的链表容器中保存了一份用户传入的值。 ...

继续学习 OpenMP 的使用，尤其是一些较新版本。 OpenMP 4.0 Controlling OpenMP thread Affinity 因为很多硬件如今是 NUMA 结构，分配线程的位置可以很大程度上影响性能。 与核绑定有关的 OpenMP 结构 proc_bind (master | close | spread) ...

写 OpenMP 的时候总是感觉怪怪的，不知道什么时候该用什么，所以最近系统化地看一遍 OpenMP 的使用，主体为 OpenMP 2.0 和 3.0。 What is OpenMP? OpenMP Model 每个线程都有可以访问全局的共享内存。 数据可以是共享的也可以是私有的。 共享的数据可以被所有线程访问。 私有数据只能被拥有它的线程访问。 数据的传递对于编程者是透明的。 同步会发生，但是它大部分时候是隐式的。 ...

华科宿舍的大门门禁用学生卡开，而每个寝室的门却只能使用钥匙打开。这就导致了每次出门都要带上学生卡和钥匙，每次回来都要先掏出卡，再掏出钥匙。这样实在是麻烦，因此我有了用校园卡就能打开宿舍门的想法。 ...

联创 Lab 组新人任务第一弹。 关于斐波那契堆 结构与特点 斐波那契堆是由一组最小堆有序树构成的。每个节点的度数为其子节点的数目。树的度数为其根节点的度数。 斐波那契堆中的树都是有根的但是无序。每个节点x包含指向父节点的指针p[x]和指向任意一个子结点的child[x]。x的所有子节点都用双向循环链表链接起来，叫做x的子链表。子链表中的每一个节点y都有指向它的左兄弟的left[y]和右兄弟的right[y]。如果节点y是x仅有的子节点，则left[y]=right[y]=y。 斐波那契堆中所有树的根节点也用一个双向循环链表链接起来。 使用一个指针指向斐波那契堆中最小元素。 斐波那契堆将操作尽可能地延后，它的插入是懒惰的，只有在不得不进行合并操作时才进行合并。在极端情况下，它甚至是一个长度很大的链表。 插入操作 将一个节点直接插入到根链表中，并比较键值的大小，如果新节点的键值小于原有节点的键值，就将斐波那契堆的指向最小节点的指针指向它。 ...

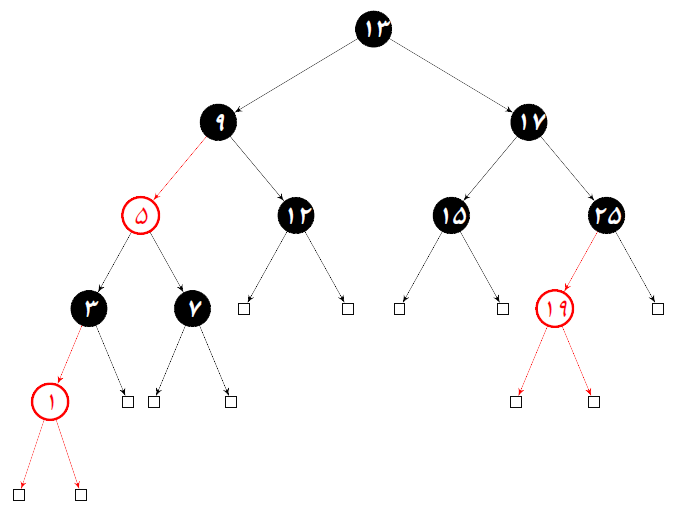
联创 Lab 组新人任务第一弹。 关于LLRB 定义 根节点是黑色的。 红色节点的儿子一定是黑色的。 任意节点到任意叶子的最短路径上都有相同数量的黑色节点。 黑色节点的儿子要么全是黑色，要么只有左儿子是黑色。 前三点与红黑树的性质相同，第四点为左偏红黑树的特殊性质，这导致了它的操作相对红黑树更加简单。 左偏红黑树也可以认为其相邻节点的边是有颜色的。 空节点的颜色认为是黑色。 插入操作 可以先就像向二叉查找树中插入节点一样操作，插入时将其颜色赋为红色。如果插入时是黑色，这会导致破坏了LLRB的平衡性质。 保持住了黑色平衡性质之后再来调整其他结构性质，要对连续两个红色节点、只有右儿子是红色节点进行旋转，对左右儿子都是红色的节点进行颜色翻转（拆分2-3-4树中的4-node）。 其操作可以是递归的，编写代码也将更加容易实现。 优先保持平衡性质的原因有：在一开始插入时保持平衡性质最容易实现（只需要给新节点赋红色），此时若优先考虑其他性质，会导致需要考虑的情况过多，而且在后续进行修补（旋转、颜色翻转）的时候不会破坏其平衡性质。 删除操作 依然优先考虑其平衡性质，删除的节点需要是红色的，因此思路就是先将需要删除的节点变成红色的。 此时需要考虑的是，如何将红色节点向下移动（向左下或右下）。当左右儿子都不是红色时也不用担心，可以通过颜色翻转实现，翻转后需要考虑移动的另一个方向是否会出现不满足左倾红黑树的情况，并对其进行修补。 由于LLRB的左偏特性，因此会出现想要向右下移动时，左儿子是红色而右儿子是黑色，因此需要对该节点进行右旋，让向右下的路径上出现红色。 当找到删除的目标节点后，如果是一个叶子节点，直接删去，如果是一个内部节点，便从它的右儿子的分支中找到最小节点与之替换，再删掉。 在向上返回的途中修补节点。 4 中判断是否为叶子节点不应该用它是否有左儿子来判断，而是用它是否有右儿子来判断，因为在前一步中有右旋操作。 ...