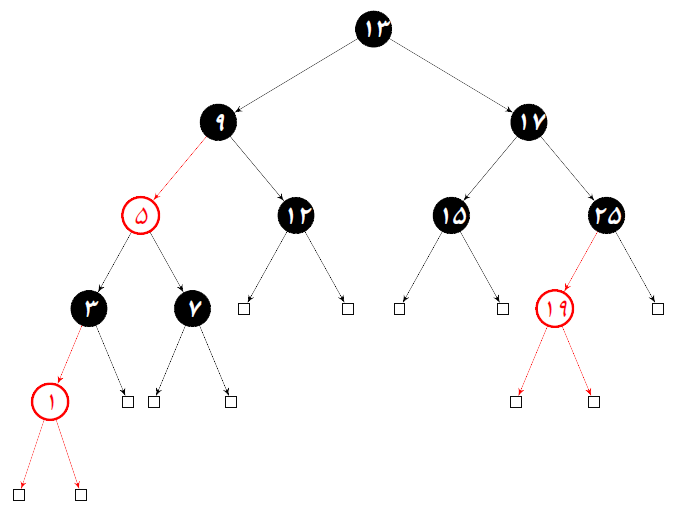
斐波那契堆
联创 Lab 组新人任务第一弹。 关于斐波那契堆 结构与特点 斐波那契堆是由一组最小堆有序树构成的。每个节点的度数为其子节点的数目。树的度数为其根节点的度数。 斐波那契堆中的树都是有根的但是无序。每个节点x包含指向父节点的指针p[x]和指向任意一个子结点的child[x]。x的所有子节点都用双向循环链表链接起来,叫做x的子链表。子链表中的每一个节点y都有指向它的左兄弟的left[y]和右兄弟的right[y]。如果节点y是x仅有的子节点,则left[y]=right[y]=y。 斐波那契堆中所有树的根节点也用一个双向循环链表链接起来。 使用一个指针指向斐波那契堆中最小元素。 斐波那契堆将操作尽可能地延后,它的插入是懒惰的,只有在不得不进行合并操作时才进行合并。在极端情况下,它甚至是一个长度很大的链表。 插入操作 将一个节点直接插入到根链表中,并比较键值的大小,如果新节点的键值小于原有节点的键值,就将斐波那契堆的指向最小节点的指针指向它。 ...